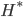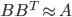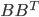This week I was at NIPS along with a big crowd of machine learning fans. It was my second NIPS, and I’m still very excited to see the advances in the field. Unfortunately, I was too busy (or too lazy?) to read on papers. Probably because I’m slow to catch up new deep net architectures. I will try to do it during the holiday and hopefully then I will put some more blog posts on interesting papers. Our group will have a “your favourite NIPS paper in 5mins” session next term and I’m very looking forward to it.
General impressions.
1. This year the number of attendants was nearly doubled to almost 6,000. 6,000! And there were even two high school students! I asked these two boys about “why you come here”, and they answered “we did some toy deep learning projects and we’re very very excited about the future of AI”. So you get the idea of “the hype of machine learning”. Next year I will definitely register and book the hotel once the registration is open!
2. Again, too many people — so no NIPS breakfast, no NIPS banquet, and in the first day I didn’t manage to talk to any poster presenters — the queues were just too long. But we did have good things — more parties by start-ups and big names, including the new players Apple and Uber. Unfortunately this year I was physically too tired that I only went to some, and it was a shame to have missed the launching party of RocketAI (which turns out to be a big big joke). Maybe it seems a bit strange that I still don’t feel that hurry on finding a job now — maybe I will be desperate of that in next year’s NIPS?
3. Hottest topics: deep RL and GANs. Everyone’s talking about it. Every company claims that they’re working on it. I admit that I’m not that crazy keen on both topics (well this summer I did spend quite a bit of time on understanding GAN objective functions), but maybe in the future I might also touch on them — who knows?
4. Tutorials were very good. I went to deep RL, computational social science, and optimisation. Deep RL was a bit strange that it assumed you know MDPs, but overall it was fairly easy to follow. Computational social science was less “high tech”, but the problem they were solving are very interesting (e.g. what makes a movie quote memorizable). Optimisation started from the very basics and slowly built on it, and I managed to follow most of the convex part. Interestingly, three tutorials (deep RL, variational inference and optimisation) had spent quite a lot of time talking about stochastic gradient and variance reduction. So we’re essentially working on very similar things!
5. Workshops were great. This year it had 50 workshops, so apparently I didn’t manage to attend most of them. But the two main workshops of my field — approximate inference and Bayesian deep learning — were actually amazing. They got 58 and 45 posters, respectively, and many of them already had very promising results. I also went to the panel of adversarial training and they had some very nice comments there.
6. Old and new friends. I’ve met quite a lot of old and new friends in this year’s NIPS. Always good to catch up and talk about random things.
7. As a guest presenter. For those who found strange that I was presenting a poster on Monday as well: my collaborator Qiang Liu was too busy presenting 3 posters on the same day, so I went to help him present the Stein variational gradient descent one. This was actually a fun experience since I don't necessary need to "sell or defend" the thing I'm presenting. Maybe another way to thoroughly understand a paper is to help its presentation at conferences?
The following are more related to my research.
1. Alpha divergences.
I didn’t expect that my proposals have been largely recognised now in the approximate inference community. Many people (more than I expected) visited my Renyi divergence poster on Wed, also quite a lot people stopped by my Saturday's constraint relaxation one. Rich had got invited to the approximate inference workshop panel talking about divergence selection. Miguel and Finale Doshi-Velez also advertised the superior performance of alpha divergence methods in the Bayesian deep learning workshop. More excitingly, I saw with my own eyes a real example of stochastic EP applied to industrial machine learning systems. I feel my hard time in the first two years really pays off. I would like to thank Rich for his excellent mentorship, and Miguel, Daniel, Thang and Mark for their great efforts.
2. Stein’s method and wild variational approximations.
Quite strangely I came to work on things related to Stein’s method and what we called “wild variational approximations”. I learned a bit about Stein’s method before, but at that time I didn't think I would use it for approximate inference. I was reviewing the operator variational inference (OPVI) paper for this year’s NIPS, at that time the paper was even harder to follow compared to its current form, and that paper still failed to convince me that Stein’s method is promising in practice. Then in August the Stein variational gradient descent paper popped out, and I really enjoyed it. I wrote a blog post on it, sent it to Qiang for comments, and suddenly the “wild variational approximation” idea came out from our mind, and we decided to collaborate on that. Apparently the OPVI authors are also very excited about it, and so this NIPS we gathered for a lunch chat and had a “cheers” for Stein’s method.
In summary, the next big thing I’m very excited about is using “truly black-box”, or “wild” (as the black box VI name has already been used by MC methods) q distributions to enhance the accuracy of approximate inference, which allows us to use probabilistic models of their full power. As the “outsider of Bayesian inference community” Ian Goodfellow pointed out in the invited talk in Bayesian deep learning workshop, it would be really nice if we can use some inference engines (e.g. neural networks) to generate (approximate) posterior samples. He talked a little bit about the ideas borrowed from GANs, which is also discussed in my approximate inference workshop submission with Qiang, and we discussed a lot more on potential directions addition to that.
I feel like “wild variational approximation” is a long-term project that is definitely impossible to be done in say several conference paper submissions, or two chapters in my thesis. But I also think I am very lucky to have found this exciting research direction, which I’d love to work on also after– my PhD study. Finally as a side note, I’m still very excited about divergences and information theoretic approaches to Bayesian inference, and I would definitely continue working on better understandings of EP-related methods, I feel like I’m also starting to put in more theoretical analysis right now, which I think is a good thing.
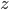
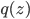
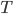
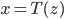
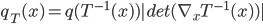
![\mathrm{KL}[q_T(x)||p(x|\mathcal{D})] - \log p(\mathcal{D})](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_4f4cf9ee67b0075216141f37d71cfe14.gif)
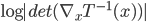
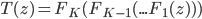
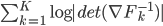
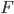
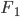
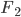
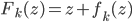
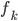
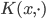
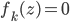
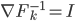
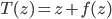
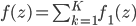
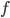
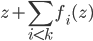
![\nabla_{f_k} \mathrm{KL}[q_{F_k} || p] |_{f_k = 0} = - \mathbb{E}_{z \sim q} [ \nabla_z K(z, \cdot) + \nabla_z \log p(z) K(z, \cdot) ]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_0fbcda61d26647608f017b8ea8003a8e.gif)
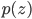
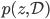
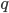
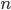
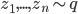
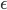
![F_k(z) = z + \frac{\epsilon}{n} \sum_n [ \nabla_{z_n} K(z_n, z) + \nabla_{z_n} \log p(z_n) K(z_n, z) ]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_458400379ef4b630d2b0e17fa3f81bf3.gif)
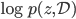
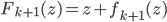
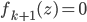
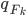
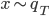
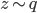
![z_i \leftarrow z_i + \frac{\epsilon}{n} \sum_n [ \nabla_{z_n} K(z_n, z_i) + \nabla_{z_n} \log p(z_n) K(z_n, z_i) ]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_01ecec148b3831efa3956017d93cded4.gif)
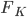
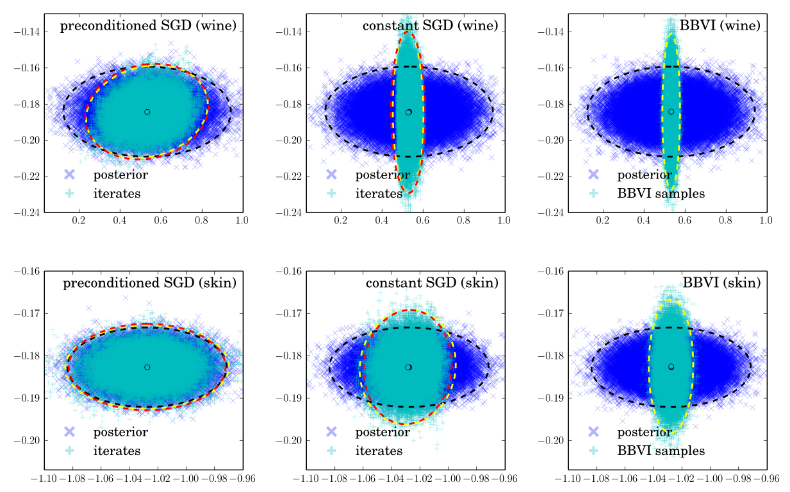
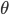
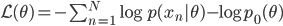
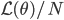
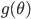
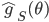
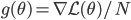
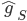
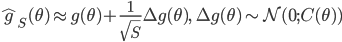
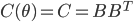

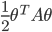
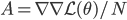
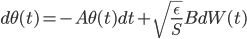
![q(\theta) \propto \exp \left[-\frac{1}{2} \theta^T \Sigma^{-1} \theta \right]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_1dd4e70879ab877ee2b3ed2b2dc7c262.gif)
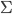
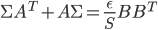
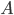
![\mathrm{KL}[q(\theta)||p(\theta|x_1, ..., x_N)]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_688b54f4781d9080e5cf384f0b175b64.gif)
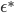
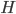
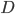
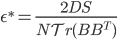
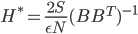
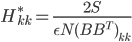
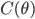
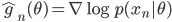
![I(\theta) = \mathbb{E}_x[\nabla \log p(x|\theta)^2]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_92488f0955aa08b95f4f9dc0ae6297e5.gif)
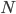
![I(\theta) = \mathbb{E}_x[-\nabla \nabla \log p(x|\theta)] = \lim_{N \rightarrow +\infty} \nabla \nabla \mathcal{L}(\theta) / N](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_eedda9e4535ffba1657000de3726a5e2.gif)