If you ask deep learning people "what is the best image generation model now", many of them would probably say "generative adversarial networks" (GAN). The original paper describes an adversarial process that asks the generator and the discriminator to fight against each other, and many people including myself like this intuition. What lessons can we learn from GAN for better approximate inference (which is my thesis topic)? I need to rewrite the framework in the language I'm comfortable with, hence I decided to put it on this blog post as a research note.
Suppose there's a machine that can show you some images. This machine flips a coin to determine what it will show to you. For heads, the machine shows you a gorgeous paint from human artists. For tails, it shows you a forged famous paint. Your job is to figure out whether the shown image is "real" or not.
Let me be precise about it using math language. Assume 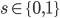 denotes the outcome of that coin flip, where 0 represents tails and 1 represents heads. The coin could possibly be a bent one so let's say your prior belief of the outcome is
denotes the outcome of that coin flip, where 0 represents tails and 1 represents heads. The coin could possibly be a bent one so let's say your prior belief of the outcome is 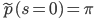 . Then the above process is summarized as the following:
. Then the above process is summarized as the following:
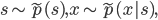
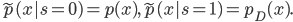
Here I use 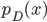 to describe the unknown data distribution and
to describe the unknown data distribution and 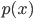 as the actual generative model we want to learn. As discussed, the generative model don't want you to know about
as the actual generative model we want to learn. As discussed, the generative model don't want you to know about 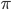 , in math this is achieved by minimizing the mutual information
, in math this is achieved by minimizing the mutual information
![\mathrm{I}[s; x] = \mathrm{KL}[\tilde{p}(s, x) || \tilde{p}(s) \tilde{p}(x)].](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_6df580dac667590c769263154aeb8030.gif)
This is quite intuitive: ![\mathrm{I}[s; x] = 0](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_e87ff28cb7ffaf246198a72d6f20c21e.gif) iff.
iff. 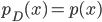 , and in this case observing an image
, and in this case observing an image 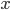 tells you nothing about the outcome of the coin flip
tells you nothing about the outcome of the coin flip 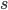 . However computing this mutual information requires evaluating
. However computing this mutual information requires evaluating 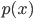 which is generally intractable. Fortunately we can use variational approximation similar to the variational information maximization algorithm. In detail we construct a lower-bound by subtracting the KL divergence:
which is generally intractable. Fortunately we can use variational approximation similar to the variational information maximization algorithm. In detail we construct a lower-bound by subtracting the KL divergence:
![\mathcal{L}[p; q] = \mathrm{I}[s; x] - \mathbb{E}_{\tilde{p}(x)}[\mathrm{KL}[\tilde{p}(s|x) ||q(s|x)] \\ = \mathrm{H}[s] + \mathbb{E}_{\tilde{p}(s, x)}[\log q(s|x)].](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_decb1089977e52be6fc2bce1e1855d00.gif)
Let's have a closer look at the equations. From the KL term we can interpret 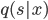 as the approximated posterior of
as the approximated posterior of 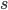 under the augmented model
under the augmented model 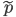 . But more interestingly
. But more interestingly 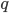 can also be viewed as the discriminator in the GAN framework. To see this, we expand the second term as
can also be viewed as the discriminator in the GAN framework. To see this, we expand the second term as
![\tilde{p}(s = 0) \mathbb{E}_{p(x)}[\log (1 - q(s = 1|x))] + \tilde{p}(s = 1) \mathbb{E}_{p_D(x)}[\log q(s = 1|x)].](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_2c99d61db085ecd2fe04b6bc75ee3bbe.gif)
Notice something familiar with? Indeed when we pick the prior as 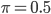 , the lower-bound
, the lower-bound ![\mathcal{L}[p; q]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_50c4f2863f9574f34d584c74904de0c6.gif) is exactly GAN's objective function (up to scaling and adding constants), and the mutual information
is exactly GAN's objective function (up to scaling and adding constants), and the mutual information ![\mathrm{I}[s; x]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_f610b226722573201d0d6e6bd94c0da3.gif) becomes the Jensen-Shannon divergence
becomes the Jensen-Shannon divergence ![\mathrm{JS}[p(x)||p_D(x)]](http://www.yingzhenli.net/home/blog/wp-content/plugins/latex/cache/tex_83f74baf9d6ce987f9a5e314fa142434.gif) , which GAN is actually minimizing.
, which GAN is actually minimizing.
To summarize, GAN can be viewed as an augmented generative model which is trained by minimizing mutual information. This augmentation is smart in the sense that it uses label-like information 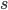 that can be obtained for free, which introduces supervision signal to help unsupervised learning.
that can be obtained for free, which introduces supervision signal to help unsupervised learning.
How useful is this interpretation? Well, in principle we can carefully design an augmented model and learn it by minimizing L2 loss/KL divergence/mutual information... you name it. But more interestingly, we can then do (automatic) divergence/algorithm selection as model selection in the "augmented" space. In the GAN example setting 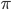 determines which JS divergence variant we use in training, e.g. see this paper. I'm not sure how useful it would be, but we can also learn
determines which JS divergence variant we use in training, e.g. see this paper. I'm not sure how useful it would be, but we can also learn 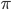 by say maximum likelihood, or even treat
by say maximum likelihood, or even treat 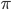 as a latent variable and put a Beta prior on it.
as a latent variable and put a Beta prior on it.
Recently I started to think about automatic algorithm selection. Probably because I'm tired of my reviewers complaining on my alpha-divergence papers "I don't know how to choose alpha and you should give us a guidance". Tom Minka gives an empirical guidance in his divergence measure tech report, and same for us in recent papers. I know this is an important but very difficult topic for research, but at least not only myself have thought about it, e.g. in this paper the authors connected beta-divergences to tweedie distributions and performed approximate maximum likelihood to select beta. Another interesting paper in this line is the "variational tempering" paper which models the annealing temperature in a probabilistic model as well. I like these papers as the core idea is very simple: we should also use probabilistic modeling for algorithmic parameters. Perhaps this also connects to Bayesian optimization but I'm gonna stop here as the note is already a bit too long.
EDIT 06/08/16:
- I briefly presented this MI interpretation (also extended to ALI) to the MLG summer reading group and you can see some notes here.
- Ferenc also posted a discussion of infoGAN with mutual information interpretation which is very nice. He also has a series of great blog posts on GANs that I wish I could have read them earlier!